1 Real Physics and Interstellar Travel
The Physics and Technology of Warp Propulsion
1.1 Classical Physics1.2 Special Relativity1.3 Twin Paradox1.4 Causality Paradox
1.5 Other Obstacles to Interstellar Travel1.6 General Relativity1.7 Examples of Relativistic Travel
1.1 Classical Physics

This chapter summarizes some very basic theorems of physics. Most of them predate the theories of special relativity and of general relativity.
Newton's laws of motion
Isaac Newton discovered the following laws. They are still valid (meaning that they are a very good approximation) for speeds much slower than the speed of light.
1. An object at rest or in uniform motion in a straight line will remain at rest or in the same uniform motion, respectively, unless acted upon by an unbalanced force. This is also known as the law of inertia.
2. The acceleration a of an object is directly proportional to the total unbalanced force F exerted on the object, and is inversely proportional to the mass m of the object (in other words, as mass increases, the acceleration has to decrease). The acceleration of an object has the same direction as the resulting force. This is also known as the law of acceleration.
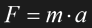
Eq. 1.1
3. If one object exerts a force on a second object, the second object exerts a force equal in magnitude and opposite in direction on the object body. This is also known as the law of interaction.
Gravitation
Two objects with a mass of m1 and m2, respectively, and a distance of r between the centers of mass, attract each other with a force F of:
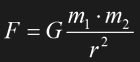
Eq. 1.2
G=6.67259*10-11m3kg-1s-2 is Newton's constant of gravitation. If an object with a mass m of much less than Earth's mass is close to Earth's surface, it is convenient to approximate Eq. 1.2 as follows:
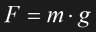
Eq. 1.3
Here g is an acceleration slightly varying throughout Earth's surface, with an average of 9.81ms-2.
Momentum conservation
In an isolated system, the total momentum is constant. This fundamental law is not affected by the theories of Relativity.
Energy conservation
In an isolated system, the total energy is constant. This fundamental law is not affected by the theories of Relativity.
Second law of thermodynamics
The overall entropy of an isolated system is always increasing. Entropy generally means disorder. An example is the heat flow from a warmer to a colder object. The entropy in the colder object will increase more than it will decrease in the warmer object. This why the reverse process, leading to lower entropy, would never take place spontaneously.
Doppler shift
If the source of the wave is moving relative to the receiver or the other way round, the received signal will have a different frequency than the original signal. In the case of sound waves, two cases have to be distinguished. In the first case, the signal source is moving with a speed v relative to the medium, mostly air, in which the sound is propagating at a speed w:
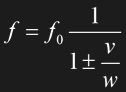
Eq. 1.4
f is the resulting frequency, f0 the original frequency. The plus sign yields a frequency decrease in case the source is moving away, the minus sign an increase if the source is approaching. If the receiver is moving relative to the air, the equations are different. If v is the speed of the receiver, then the following applies to the frequency:
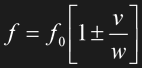
Eq. 1.5
Here the plus sign denotes the case of an approaching receiver and an according frequency increase; the minus sign applies to a receiver that moves away, resulting in a lower frequency.
The substantial difference between the two cases of moving transmitter and moving receiver is due to the fact that sound needs air in order to propagate. Special relativity will show that the situation is different for light. There is no medium, no "ether" in which light propagates and the two equations will merge to one relativistic Doppler shift.
Particle-wave dualism
In addition to Einstein's equivalence of mass and energy (see 1.2 Special Relativity), de Broglie unified the two terms in that any particle exists not only alternatively but even simultaneously as matter and radiation. A particlewith a mass m and a speed v was found to be equivalent to a wave with a wavelength lambda. With h, Planck's constant, the relation is as follows:
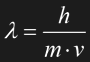
Eq. 1.6
The best-known example is the photon, a particle that represents electromagnetic radiation. The other way round, electrons, formerly known to have particle properties only, were found to show a diffraction pattern which would be only possible for a wave. The particle-wave dualism is an important prerequisite to quantum mechanics.
1.2 Special Relativity
Special relativity (SR) doesn't play a role in our daily life. Its impact becomes apparent only for relative speeds that are considerable fractions of the speed of light, c. I will henceforth occasionally refer to them as "relativistic speeds". The effects were first measured as late as towards the end of the 19th century and explained by Albert Einstein in 1905.
Side note There are many approaches in literature and in the web to explain special relativity. Please refer to the appendix. A very good reference from which I have taken several suggestions is Jason Hinson's article on Relativity and FTL travel [Hin1]. You may wish to read his article in parallel.
The whole theory is based on two postulates:
1. There is no invariant "fabric of space" or "ether" relative to which an absolute speed could be defined or measured. The terms "moving" or "resting" make only sense if they refer to a certain other frame of reference. The perception of movement is always mutual; the starship pilot who leaves Earth could claim that he is actually resting while the solar system is moving away.
2. The speed of light, c=3*108m/s in the vacuum, is the same in all directions and in all frames of reference. This means that nothing is added or subtracted to this speed as the light source apparently moves.
Frames of reference
In order to explain special relativity, it is crucial to introduce frames of reference. Such a frame of reference is basically a point-of-view, something inherent to an individual observer who perceives an event from a certain angle. The concept is in some way similar to the trivial spatial parallax where two or more persons see the same scene from different spatial angles and therefore give different descriptions of it. However, the following considerations are somewhat more abstract. "Seeing" or "observing" will not necessarily mean a sensory perception. On the contrary, the observer is assumed to take into consideration every "classic" measurement error such as signal delay or Doppler shift.
Aside from these effects that can be rather easily handled mathematically there is actually one even more severe constraint. The considerations on special relativity require inertial frames of reference. According to the definition in the general relativity chapter, this would be a floating or free falling frame of reference. Any presence of gravitational or acceleration forces would not only spoil the measurement, but could ultimately even question the validity of the SR. One provision for the following considerations is that all observers should float within their starships in space so that they can be regarded as local inertial frames. Basically, every observer has their own frame of reference; two observers are in the same frame if their relative motion to a third frame is the same, regardless of their distance.
Space-time diagram
Special relativity takes place in the four-dimensional space-time. In an inertial frame all the Cartesian spatial coordinates x, y and z are equivalent (there is no "up" and "down" in space in a total absence of gravitational forces). Hence, for the sake of simplicity, we may substitute the three axes with one generic horizontal space (x-) axis which may stand for any of the coordinates x,y,z or all of them. Together with the vertical time (t-) axis we obtain a two-dimensional diagram (Fig. 1.1). It is very convenient to give the distance in light-years and the time in years. Irrespective of the current frame of reference, the speed of light always equals c and would be exactly 1ly per year in our diagram, according to the second postulate. Any light beam will therefore always form an angle of either 45° or -45° with the x-axis and the t-axis, as indicated by the yellow lines.

Fig. 1.1 Space-time diagram for a resting observer
A resting observer O (or better: an observer who thinks to be resting) draws an exactly perpendicular x-t-diagram for himself. The x-axis is equivalent to t=0 and is therefore a line of simultaneity, meaning that for O everything located on this line is simultaneous. This applies to every horizontal line t=const. likewise. The t-axis and every line parallel to it denote x=const. and therefore no movement in this frame of reference. If O is to describe the movement of another observer O* with respect to himself, O*'s time axis t* is sloped, and the reciprocal slope indicates a certain speed v=x/t. Fig. 1.2 shows O's coordinate system in gray, and O*'s in O's view in white. The common origin denotes that O and O* pass by each other (x=x*=0) at the time t=t*=0. At the first glance it seems strange that O*'s x*-axis is sloped into the opposite direction than his t*-axis, distorting his coordinate system.

Fig. 1.2 Space-time diagram for a resting and a moving observer

Fig. 1.3 Sloped x*-axis of a moving observer
The x*-axis can be explained by assuming two events A and B occurring at t*=0 at some distance to the two observers, as depicted in Fig. 1.3. O* sees them simultaneously, whereas O sees them at two different times. Since the two events are simultaneous in O*'s frame, the line A-0-B defines his x*-axis. A and B might be located anywhere on the 45-degree light paths traced back from the point "O* sees A&B", so we need further information to actually locate A and B. Since O* is supposed to actually *see* them at the same time (and not only date them back to t*=0), we also know that the two events A and B must have the same distance from the origin of the coordinate system. Now A and B are definite, and connecting them gives us the x*-axis. Some simple trigonometry would reveal that actually the angle between x* and x is the same as between t* and t, only the direction is opposite.
The faster the moving observer is, the closer will the two axes t* and x* move to each other. It becomes obvious in Fig. 1.2 that finally, at v=c, they will merge to one single axis, equivalent to the path of a light beam.
Time dilation
The above space-time diagrams don't have a scale on the x*- and t*-axes so far. It is not the same scale as on the x- and t-axis, respectively. The method of determining the t*-scale is illustrated in the upper left half of Fig. 1.4. When the moving observer O* passes the resting observer O, they both set their clocks to t*=0 and t=0, respectively. Some time later, O's clock shows t=3, and at a yet unknown instant O*'s clock shows t*=3. The yellow light paths show when O will actually *see* O*'s clock at t*=3 (which is obviously after his own t=3 because the light needs time to travel), and vice versa. If O is smart enough, he can calculate the time when this light was emitted (by tracing back the -45° yellow line to O*'s t*-axis). His lines of simultaneity are exactly horizontal (red line), and the reconstructed event "t*=3" will take place at some yet unknown time on his t-axis. And even though O has taken into account the speed of light, "t*=3" still happens later than t=3. The quotation marks distinguish O's reconstruction of "t*=3" and O*'s direct reading t*=3. O* will do the same by reconstructing the event "t=3" (green line), which happens after his own t*=3. In other words, just as O sees the time of O* dilated, O* can say the same about O's time.

Fig. 1.4 Illustration of time dilation (upper left half) and length contraction (lower right half)
Since O*'s x*-axis and therefore his green line of simultaneity is sloped while the x-axis is not, it is impossible that any two events t=3 and "t*=3" and the two corresponding events t*=3 and "t=3" are simultaneous (and would occupy a single point) on the respective t-axis. If there is no absolute simultaneity, at least one of the two observers would see the other one's time dilated (in slow motion). Now we have to apply the first postulate, the principle of relativity. There must not be any preferred frame of reference, all observations have to be mutual. Either observer sees the other one's time dilated by the same factor. Not only in this example, but always. In our diagram the red and the green line have to cross to fulfill this postulate. More precisely, the ratio "t*=3" to t=3 has to be equal to "t=3" to t*=3. Some further calculations yield the following time dilation:
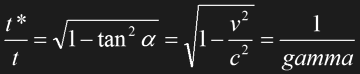
Eq. 1.7
Side note When drawing the axes to scale in an x-t diagram, one has to account for the inherently longer hypotenuse t* and multiply the above formula with an additional factor cos alpha to "project" t* on t.
Note that the time dilation would be the square root of a negative number (imaginary) if we assume an FTL speed v>c. Imaginary numbers are not really forbidden, on the contrary, they play an important role in the description of waves. Anyway, a physical quantity such as the time doesn't make any sense once it gets imaginary. Unless a suited interpretation or a more comprehensive theory is found, considerations end as soon as a time (dilation), which has to be finite and real by definition, would become infinitely large or imaginary. The same applies to the length contraction and mass increase. Star Trek's warp theory (although it does not really have a mathematical description) circumvents all these problems in a way that no such relativistic effects occur.
Length contraction
The considerations for the scale of the x*-axis are similar as those for the t*-axis. They are illustrated in the bottom right portion of Fig. 1.4. Let us assume that O and O* both have identical rulers and hold their left ends x=x*=0 when they meet at t=t*=0. Their right ends are at x=l on the x-axis and at x*=l on the x*-axis, respectively. O and his ruler rest in their frame of reference. At t*=0 (which is not simultaneous with t=0 at the right end of the ruler!) O* obtains a still unknown length "x=l" for O's ruler (green line). O* and his ruler move along the t*-axis. At t=0, O sees an apparent length "x=l" of O*'s ruler (red line). Due to the slope of the t*-axis, it is impossible that the two observers mutually see the same length l for the other ruler. Since the relativity principle would be violated in case one observer saw two equal lengths and the other one two different lengths, the mutual length contraction must be the same. Note that the geometry is virtually the same as for the time dilation, so it's not astounding that length contraction is determined by the factor gamma too:
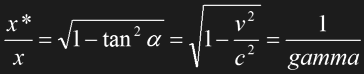
Eq. 1.8
Side note Once again, note that when drawing the x*-axis to scale, a correction is necessary, a factor of cos alpha to the above formula.
Addition of velocities
One of the most popular examples used to illustrate the effects of special relativity is the addition of velocities. It is obvious that in the realm of very slow speeds it's possible to simply add or subtract velocity vectors from each other. For simplicity, let's assume movements that take place in only one dimension so that the vector is reduced to a plus or minus sign along with the absolute speed figure, like in the space-time diagrams. Imagine a tank that has a speed of v compared to the ground and to an observer standing on the ground (Fig. 1.5). The tank fires a projectile whose speed is determined as w by the tank driver. The resting observer, on the other hand, will register a projectile speed of v+w relative to the ground. So far, so good.

Fig. 1.5 Non-relativistic addition of velocities

Fig. 1.6 Relativistic addition of velocities
The simple addition (or subtraction, if the speeds have opposite directions) seems very obvious, but it isn't so if the single speeds are considerable fractions of c. Let's replace the tank with a starship (which is intentionally a generic vessel, no Trek ship), the projectile with a laser beam and assume that both observers are floating, one in open space and one in his uniformly moving rocket (no acceleration), at a speed of c/2 compared to the first observer (Fig. 1.6). The rocket pilot will see the laser beam move away at exactly c. This is still exactly what we expect. However, the observer in open space won't see the light beam travel at v+c=1.5c but only at c. Actually, any observer with any velocity (or in any frame of reference) would measure a light speed of exactly c=3*108m/s.
Space-time-diagrams allow to derive the addition theorem for relativistic velocities. The resulting speed u is given by:
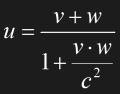
Eq. 1.9
For v,w<<c we may neglect the second term in the denominator. We obtain u=v+w as we expect it for small speeds. If vw gets close to c2, the speed u may be close to, but never equal to or even faster than c. Finally, if either v or w equals c, u is equal to c as well. There is obviously something special to the speed of light. c always remains constant, no matter where in which frame and which direction it is measured. c is also the absolute upper limit of all velocity additions and can't be exceeded in any frame of reference.
Mass increase
Mass is a property inherent to any kind of matter. We may distinguish two forms of mass, one that determines the force that has to be applied to accelerate an object (inert mass) and one that determines which force it experiences in a gravitational field (heavy mass). At latest since the equivalence principle of GR they have been found to be absolutely identical.
However, mass is apparently not an invariant property. Consider two identical rockets that lifted off together at t=0 and now move away from the launch platform in opposite directions, each with a constant absolute speed of v. Each pilot sees the launch platform move away at v, while Eq. 1.9 shows us that the two ships move away from each other at a speed u<2v. The "real" center of mass of the whole system of the two ships would be still at the launch platform, however, each pilot would see a center of mass closer to the other ship than to his own. This may be interpreted as a mass increase of the other ship to m compared to the rest mass m0 measured for both ships prior to the launch:
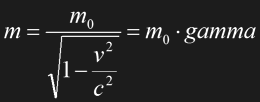
Eq. 1.10
This function is plotted in Fig. 1.7.
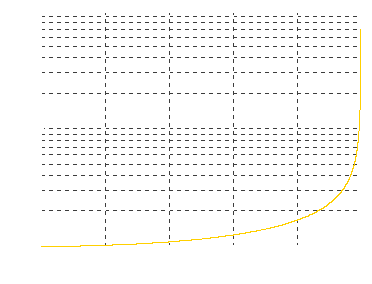
Fig. 1.7 Mass increase for relativistic speeds
So each object has a rest mass m0 and an additional mass m-m0 due to its speed as seen from another frame of reference. This is actually a convenient explanation for the fact that the speed of light cannot be reached. The mass increases more and more as the object approaches c, and so would the required momentum to propel the ship.
Finally, at v=c, we would get an infinite mass, unless the rest mass m0 is zero. The latter must be the case for photons which always move at the speed of light, which even define the speed of light. If we assume an FTL speed v>c, the denominator will be the square root of a negative number, and therefore the whole mass will be imaginary. As already stated for the time dilation, there is not yet a suitable theory how an imaginary mass could be interpreted.
Mass-energy equivalence
Let us consider Eq. 1.10 again. It is possible to express it as follows:
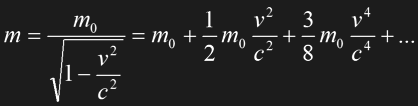
Eq. 1.11
It is obvious that we may neglect the third order and the following terms for slow speeds. If we multiply the equation with c2 we obtain the familiar Newtonian kinetic energy ½m0v2 plus a new term m0c2. Obviously already the resting object has a certain energy content m0c2. We get a more general expression for the complete energy E contained in an object with a rest mass m0 and a moving mass m, so we may write (drumroll!):
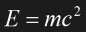
Eq. 1.12
Energy E and mass m are equivalent; the only difference between them is the constant factor c2. If there is an according energy to each given mass, can the mass be converted to energy? The answer is yes, and Trek fans know that the solution is a matter/antimatter reaction in which the two forms of matter annihilate each other, thereby transforming their whole mass into energy.
Light cone
Let us have a look at Fig. 1.1 again. There are two light beams running through the origin of the diagram, one traveling in positive and one in negative x direction. The slope is 1ly per year, which equals c. If nothing can move faster than light, then every t*-axis of a moving observer and every path of a message sent from one point to another in the diagram must be steeper than these two lines. This defines an area "inside" the two light beams for possible signal paths originating at or going to (x=0,t=0). This area is marked dark green in Fig. 1.8. The black area is "outside" the light cone. The origin of the diagram marks "here (x=0)" and "now (t=0)" for the resting observer.

Fig. 1.8 The light cone
The common-sense definition tells us that "future" is any event at t>0, and past is any event at t<0. Special relativity shows us a different view of these two terms. Let us consider the four marked events which could be star explosions (novae), for instance. Event A is below the x-axis and within the light cone. It is possible for the resting observer O to see or to learn about the event in the past, since a -45° light beam would reach the t-axis at about one and a half years prior to t=0. Therefore this event belongs to O's past. Event B is also below the x-axis, but outside the light cone. The event has no effect on O in the present, since the light would need almost another year to reach him. Strictly speaking, B is not in O's past. Similar considerations are possible for the term "future". Since his signal wouldn't be able to reach the event C, outside the light cone, in time, O is not able to influence it. It's not in his future. Event D, on the other hand, is inside the light cone and may therefore be caused or influenced by the observer.
What about a moving observer? One important consequence of the considerations in this whole chapter was that two different observers will disagree about where and when a certain event happens. The light cone, on the other hand, remains the same, irrespective of the frame of reference. So even if two observers meeting at t=0 have different impressions about simultaneity, they will agree that there are certain, either affected (future) or affecting (past) events inside the light cone, and outside events they shouldn't bother about.
1.3 Twin Paradox
The considerations about the time dilation in special relativity had the result that the terms "moving observer" and "resting observer" are interchangeable as are their space-time diagrams. If there are two observers with a speed relative to each other, either of them will see the other one move. Either observer will see the other one's clock ticking slower. Special relativity necessarily requires that the observations are mutual, since it forbids a preferred, absolutely resting frame of reference. Either clock is slower than the other one? How is this possible?
The problem
Specifically, the twin paradox is about twins of whom one travels to the stars at a relativistic speed, while the other one stays on Earth. It is obvious that the example assumes twins, since it would be easier to see if one of them actually looks older than the other one when they meet again. Anyway, it should work with unrelated persons as well. What happens when the space traveler returns to Earth? Is he the younger one, or maybe his twin on Earth, or are they equally old?
Side note The following example for the twin paradox deliberately uses the same figures as Jason Hinson's excellent treatise on Relativity and FTL travel [Hin1], to increase the chance of understanding it. And because I was too lazy to recalculate everything. ;-)
To anticipate the result, the space traveler will be the younger one when he returns. The solution is almost trivial. Time dilation only remains the same as long as both observers stay in their respective frames of reference. However, if the two observers want to meet again, one of them or both of them have to change their frame (s) of reference. In this case it is the space traveler who has to decelerate, turn around, and accelerate his starship in the other direction. It is important to note that the whole effect can be explained without referring to any general relativity effects. Time dilation attributed to acceleration or gravity will change the result, but it will not play a role in the following discussion. The twin paradox is not really paradox, it can be solved, and this is best done with a space-time diagram.
Part 1: moving away from Earth
Fig. 1.9 shows the first part of the FTL travel. O is the "resting" observer who stays on Earth the whole time. Earth is subsequently regarded as an approximated inertial frame. Strictly speaking, O would have to float in Earth's orbit, according to the definition in general relativity. Once again, however, it is important to say that the following considerations don't need general relativity at all. I only refer to O as staying in an inertial frame so as to exclude any GR influence.

Fig. 1.9 Illustration of the twin paradox, moving away from Earth
The moving observer O* is supposed to travel at a speed of 0.6c relative to Earth and O. When O* passes by O (x=x*=0), they both set their clocks to zero (t=t*=0). So the origin of their space-time diagrams is the same, and the time dilation will become apparent in the different times t* and t for simultaneous events. As outlined above, t* is sloped, as is x* (see also Fig. 1.3). The measurement of time dilation works as outlined in Fig. 1.4. O's lines of simultaneity are parallel to his x-axis and perpendicular to his t-axis. He will see that 5 years on his t-axis correspond with only 4 years on the t*-axis (red arrow), because the latter is stretched according to Eq. 1.7. Therefore O*'s clock is ticking slower from O's point-of-view. The other way round, O* draws lines of simultaneity parallel to his sloped x*-axis and he reckons that O's clock is running slower, 4 years on his t*-axis compared to 3.2 years on the t-axis (green arrow). It is easy to see that the mutual dilation is the same, since 5/4 equals 4/3.2. Who is correct? Answer: Both of them, since they are in different frames of reference, and they stay in these frames. The two observers just see things differently; they wouldn't have to care whether their perception is "correct" and the other one is actually aging slower -- unless they wanted to meet again.
Part 2: resting in space
Now let us assume that O* stops his starship when his clock shows t*=4 years, maybe to examine a phenomenon or to land on a planet. According to Fig. 1.10 he is now resting in space relative to Earth and his new x**-t** coordinate system is parallel to the x-t system of O on Earth. O* is now in the same frame of reference as O. And this is exactly the point: O*'s clock still shows 4 years, and he notices that not 3.2 years have elapsed on Earth as briefly before his stop, but 5 years, and this is exactly what O says too. Two observers in the same frame agree about their clock readings. O* has been in a different frame of reference at 0.6c for 4 years of his time and 5 years of O's time. This difference becomes a permanent offset when O* enters O's frame of reference. Paradox solved.

Fig. 1.10 Illustration of the twin paradox, landing or resting in space
It is obvious that the accumulative dilation effect will become the larger the longer the travel duration is. Note that O's clock has always been ticking slower in O*'s moving frame of reference. The fact that O's clock nevertheless suddenly shows a much later time (namely 5 instead of 3.2 years) is solely attributed to the fact that O* is entering a frame of reference in which exactly these 5 years have elapsed.
Once again, it is crucial to annotate that the process of decelerating would only change the result qualitatively, since there could be no exact kink, as O* changes from t* to t**. Practical deceleration is no sudden process, and the transition from t* to t** should be curved. Moreover, the deceleration itself would be connected with a time dilation according to GR, but the paradox is already solved without taking this into account.
Part 3: return to Earth
Let us assume that at t*=4 years, O* suddenly gets homesick and turns around immediately instead of just resting in space. His relative speed is v=-0.6c during his travel back to Earth, the minus sign indicating that he is heading to the negative x direction. It is obvious that this second part of his travel should be symmetrical to the first part at +0.6c in Fig. 1.9, the symmetry axis being the clock comparison at t=5 years and t**=4 years. This is exactly the moment when O* has covered both half of his way and half of his time.

Fig. 1.11 Illustration of the twin paradox, return to Earth
Fig. 1.11 demonstrates what happens to O*'s clock comparison. Since he is changing his frame of reference from v=0.6c to v=-0.6c relative to Earth, the speed change and therefore the effect is twice as large as in Fig. 1.10. Assuming that O* doesn't stop for a clock comparison as he did above, he would see that O's clock directly jumps from 3.2 years to 6.8 years. Following O*'s travel back to Earth, we see that the end time is t**=8 years (O*'s clock) and t=10 years (O's clock). The traveling twin is actually two years younger at their family reunion.
We could imagine several other scenarios in which O might catch up with the traveling O*, so that O is actually the younger one. Alternatively, O* could stop in space, and O could do the same travel as O*, so that they would be equally old when O reaches O*. The analysis of the twin paradox shows that the simple statement "moving observers age slower" is insufficient. The statement has to be modified in that "moving observers age slower as seen from any different frame of reference, and they notice it when they enter this frame themselves".
1.4 Causality Paradox
As already stated further above, two observers in different frames of reference will disagree about the simultaneity of certain events (see Fig. 1.3). What if the same event were in one observer's future, but in another observer's past when they meet each other? This is not a problem in special relativity, since no signal is allowed to travel faster than light. Any event that could be theoretically influenced by one observer, but has already happened for the other one, is outside the light cone depicted in Fig. 1.8. Causality is preserved.
Fig. 1.12 depicts the space-time diagrams of two observers with a speed relative to each other. Let us assume the usual case that the moving observer O* passes by the resting observer O at t=t*=0. They agree about the simultaneity of this passing event, but not about any other event at t<>0 or t*<>0. Event A is below the t-axis, but above the t*-axis. This doesn't matter as long as the two can send and receive only STL signals. Event A is outside the light cone, and the argument would be as follows: A is in O*'s future (future in a wider sense), but he has no means of influencing it at t*=0, since his signal couldn't reach it in time. A is in O's past (past in a wider sense), but it doesn't matter because he can't know of it at t=0.
What would be different if either FTL travel or FTL signal transfer were possible? In this case we would be allowed to draw signal paths of less than 45 degrees steepness in the space-time diagram. Let us assume that O* is able to send an FTL signal to influence or to cause event A in the first place, just when the two observers pass each other. Note that this signal would travel at v>c in any frame of reference, and that it would travel back in time in O's frame, since it runs into negative t-direction in O's orthogonal x-t coordinate system, to an event that is in O's past. If O* can send an FTL signal to cause the event A, then a second FTL signal can be sent to O to inform him of A as soon as it has just happened. This signal would run at v>c in positive t-direction for O, but in negative t*-direction for O*. So the situation is exactly inverse to the first FTL signal. Now O is able to receive a message from O*'s future.

Fig. 1.12 Illustration of a possible causality paradox
The paradox occurs when O, knowing about the future, decides to prevent A from happening. Maybe O* is a bad guy, and event A is the death of an unfortunate victim, killed because of his FTL message. O would have enough time to hinder O*, to warn the victim or to take other precautions, since it is still t<0 when he receives the message, and O* has not yet caused event A.
The sequence of events (in logical rather than chronological order) would be as follows:
1. At t=t*=0, the two observers pass each other and O* sends an FTL message that causes A.
2. A happens in O*'s past (t*<0) and in O's future (t>0).
3. O learns about event A through another FTL signal, still at t<0, before he meets O*.
4. O might be able to prevent A from happening. However, how could O have learned about A if it actually never happened?
This is obviously the SR version of the well-known grandfather paradox. Note that these considerations don't take into account which method of FTL travel or FTL signal transfer is used. Within the realm of special relativity, they should apply to any form of FTL travel. Anyway, if FTL travel is feasible, then it is much like time travel. It is not clear how this paradox can be resolved. The basic suggestions are the same as for generic time travel and are outlined in my time travel article.
1.5 Other Obstacles to Interstellar Travel
Power considerations
Rocket propulsion (as a generic term for any drive using accelerated particles) can be described by momentum conservation, resulting in the following simple equation:
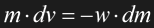
Eq. 1.13
The left side represents the infinitesimal speed increase (acceleration) dv of the ship with a mass m, the right side is the mass decrease -dm of the ship if particles are thrusted out at a speed w. This would result in a constant thrust and therefore in a constant acceleration, at least in the range of ship speeds much smaller than c. Eq. 1.13 can be integrated to show the relation between an initial mass m0, a final mass m1 and a speed v1 to be achieved:
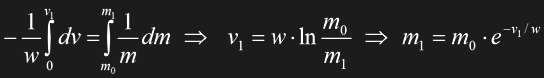
Eq. 1.14
The remaining mass m1 at the end of the flight, the payload, is only a fraction of the total mass m0, the rest is the necessary fuel. The achievable speed v1 is limited by the speed w of the accelerated particles, i.e. the principle of the drive, and by the fuel-to-payload ratio.
Let us assume a photon drive as the most advanced conventional propulsion technology, so that w would be equal to c, the speed of light. The fuel would be matter and antimatter in the ideal case, yielding an efficiency near 100%, meaning that according to Eq. 1.14 almost the complete mass of the fuel could contribute to propulsion. Eq. 1.13 and Eq. 1.14 would remain valid, with w=c. If relativistic effects are not yet taken into account, the payload could be as much as 60% of the total mass of the starship, if it's going to be accelerated to 0.5c. However, the mass increase at high sublight speeds as given in Eq. 1.10 spoils the efficiency of any available propulsion system as soon as the speed gets close to c, since the same thrust will effect a smaller acceleration. STL examples will be discussed in Section 1.7.
Acceleration and Deceleration
Eq. 1.13 shows that the achievable speed is limited by the momentum (speed and mass) of the accelerated particles, provided that a conventional rocket engine is used. The requirements of such a drive, e.g. the photon drive outlined above, are that a considerable amount of particles has to be accelerated to a high speed at a satisfactory efficiency.
Even more restrictively, the human body simply couldn't sustain accelerations of much more than g=9.81ms-2, which is the acceleration on Earth's surface. Accelerations of several g are taken into account in aeronautics and astronautics only for short terms, with critical peak values of up to 20g. Unless something like Star Trek's IDF (inertial damping field) will be invented [Ste91], it is probably the most realistic approach to assume a constant acceleration of g from the traveler's viewpoint during the whole journey. This would have the convenient side effect that an artificial gravity equal to Earth's surface would be automatically created.

Fig. 1.13 Concept of the turn-around starship
According to Newton's first and second postulates it will be necessary to decelerate the starship as it approaches the destination. Thus, the starship needs a "brake". It wouldn't be very wise to install a second, equally powerful engine at the front of the starship for this purpose. Moreover, the artificial gravity would act in the opposite direction during the deceleration phase in this case. The alternative solution is simple: Half-way to the destination, the starship would be simply turned around by means of maneuvering thrusters so that it now decelerates at a rate of g; the artificial gravity would remain exactly the same. Actually, complying with the equivalence principle of general relativity, if the travelers didn't look out of the windows or at their sensor readings, they wouldn't even notice that the ship is now decelerating. Only during the turn-around the gravity would change for a brief time while the main engines are switched off. Fig. 1.13 depicts such a turn-around ship, "1." is the acceleration phase, "2." the turn-around, "3." the deceleration.
Doppler shift
In the chapter on classical physics, the Doppler effect has been described as the frequency increase or decrease of a sound wave. The two cases of a moving source and moving observer only have to be distinguished in case of an acoustic signal, because the speed of sound is constant relative to the air and therefore the observer would measure different signal speeds in the two cases. Since the speed of light is constant, there is only one formula for Doppler shift of electromagnetic radiation, already taking into account SR time dilation:
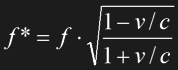
Eq. 1.15
Note that Eq. 1.15 covers both cases of frequency increase (v and c in opposite directions, v/c<0) and frequency decrease (v and c in the same direction, v/c>0). Since the power of the radiation is proportional to its frequency, the forward end will be subject to a higher radiation power and dose than the rear end, assuming isotropic (homogeneous) radiation.
Actually, for STL travel the Doppler shift is not exactly a problem. At 0.8c, for instance, the radiation power at the bow is three times the average of the isotropic radiation. Visible light would "mutate" to UV radiation, but its intensity would still be far from dangerous. Only if v gets very close to c (or -c, to be precise), the situation could get critical for the space travelers, and an additional shielding would be necessary. On the other hand, it's useless anyway to get as close to c as possible because of the mass increase. For v=-c, the Doppler shift would be theoretically infinite.
It is not completely clear (but may become clear in one of the following chapters) how Doppler shift can be described for an FTL drive in general or warp propulsion in particular. It could be the conventional, non-relativistic Doppler shift that applies to warp drive since mass increase and time dilation are not valid either. In this case the radiation frequency would simply increase to 1+|v/c| times the original frequency, and this could be a considerable problem for high warp speeds, and it would require thick radiation shields and forbid forward windows.
1.6 General Relativity
As we can infer from the name, general relativity (GR) is a more comprehensive theory than special relativity. Although the concept as a whole has to be explained with massive use of complex mathematics, the basic principles are quite evident and perhaps easier to understand than those of special relativity. General relativity takes into account the influence of the presence of a mass, of gravitational fields caused by this mass.
Inertial frames
The chapter on special relativity assumed inertial frames of reference, that is, frames of reference in which there is no acceleration to the object under investigation. The first thought might be that a person standing on Earth's surface should be in an inertial frame of reference, since he is not accelerated relative to Earth. This idea is wrong, according to GR. Earth's gravity "spoils" the possible inertial frame. Although this is not exactly what we understand as "acceleration", there can't be an inertial frame on Earth's surface. Actually, we have to extend our definition of an inertial frame.
Principle of equivalence
Consider the rocket in the left half of Fig. 1.14 whose engines are powered somewhere in open space, far away from any star or planet. According to Newton's Second Law of Motion (see 1.1 Classical Physics), if the engine force is constant the acceleration will be constant too. The thrust may be adjusted in a way that the acceleration is exactly g=9.81ms-2, equal to the acceleration in Earth's gravitational field. The passenger will then be able to stand on the rocket's bottom as if it were Earth's surface, since the floor of the rocket exerts exactly the same force on him in both cases. Compare it to the right half of Fig. 1.14; the two situations are equivalent. "Heavy mass" and "inert mass" are actually the same.
One might object that there should still be many differences. Specifically one should expect that a physicist who is locked up in such a starship (without windows) should be able to find out whether it is standing on Earth or accelerating in space. The surprising result of GR is that he will get exactly the same experimental results in both cases. Imagine that the rocket is quite long, and our physicist sends out a laser beam from the rocket's bottom to its top. In the case of the accelerating rocket we would not be surprised that the frequency of the light beam decreases, since the receiver would virtually move away from the source while the beam is on the way. This effect is the familiar Doppler shift. We wouldn't expect the light frequency (and therefore its intensity) to decrease inside a stationary rocket too, but that's exactly what happens in Earth's gravitational field! The light beam has to "climb up" in the field, thereby losing energy, which becomes apparent in a lower frequency. Obviously, as opposed to common belief so far, light is affected by gravity.

Fig. 1.14 Equivalence of rocket standing on Earth
and rocket accelerated in space (no inertial frames)

Fig. 1.15 Equivalence of free falling rocket
and rocket floating in space (inertial frames)
Let us have a look at Fig. 1.15. The left half shows a rocket floating in space, far away from any star or planet. No force acts upon the passenger, he is weightless. It's not only a balance of forces, but all forces are actually zero. This is an inertial frame, or at least a very good approximation thereof. There can be obviously no perfect inertial frame as long as there is still a certain mass present. Compare this to the depiction of the free falling starship in the right half of Fig. 1.15. Both the rocket and the passenger are attracted with the same acceleration a=g. Although there is acceleration, this is an inertial frame too, and it is equivalent to the floating rocket. The point is that in both cases the inside of the rocket is an inertial frame, since the ship and passenger don't exert any force/acceleration on each other. About the same applies to a parabolic flight or a ship in orbit during which the passengers are weightless.
We might have found an inertial frame also in the presence of a mass, but we have to keep in mind that this can be only an approximation. Consider a very long ship falling down to Earth. The passenger in the rocket's top would experience a smaller acceleration than the rocket's bottom and would have the impression that the bottom is accelerated with respect to himself. Similarly, in a very wide rocket (it may be the same one, only turned by 90 degrees), two people at either end would see that the other one is accelerated towards him. This is because they would fall in slightly different radial directions to the center of mass. None of these observations would be allowed within an inertial frame. Therefore, we are only able to define local inertial frames.
Time dilation
As already mentioned above, there is a time dilation in general relativity, because light will gain or lose potential energy when it is moving farther away from or closer to a center of mass, respectively. The time dilation depends on the gravitational potential as given in Eq. 1.2 and amounts to:
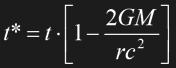
Eq. 1.16
G is Newton's gravitational constant, M is the planet's mass, and r is the distance from the center of mass. Eq. 1.16 can be approximated in the direct vicinity of the planet using Eq. 1.3:
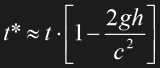
Eq. 1.17
In both equations t* is the time elapsing on the surface, while t is the time in a height h above the surface, with g being the standard acceleration. The time t* is always shorter than t so that, theoretically, people living on the sea level age slower than those in the mountains. The time dilation has been measured on normal plane flights and summed up to 52.8 nanoseconds when the clock on the plane was compared to the reference clock on the surface after 40 hours [Sex87]. 5.7 nanoseconds had to be subtracted from this result, since they were attributed to the time dilation of relativistic movements that was discussed in the chapter about special relativity.
Curved space
The time dilation in the above paragraph goes along with a length contraction in the vicinity of a mass:
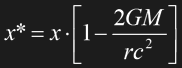
Eq. 1.18
However, length contraction is not a commonly used concept in GR. The equivalent idea of a curved space is usually preferred. For it is obviously impossible to illustrate the distortions of a four-dimensional space-time, we have to restrict our considerations to two spatial dimensions. Imagine two-dimensional creatures living on an even plastic foil. The creatures might have developed a plane geometry that allows them to calculate distances and angles. Now someone from the three-dimensional world bends and stretches the plastic foil. The two-dimensional creatures will be very confused about it, since their whole knowledge of geometry doesn't seem to be correct anymore. They might apply correction factors in certain areas, compensating for points that are measured as being closer together or farther away from each other than their calculations indicate. Alternatively, a very smart two-dimensional scientist might come up with the idea that their area is actually not flat but warped. About this is what general relativity says about our four-dimensional space-time.

Fig. 1.16 Illustration of curved space
Fig. 1.16 is limited to the two spatial dimensions x and y. It can be regarded as something like a "cross-section" of the actual spatial distortion. We can imagine that the center of mass is somewhere in the middle "underneath" the x-y plane, where the curvature is most pronounced (a "gravity well").
Speed of light
A light beam passing by an area with strong gravity such as a star will not be "straight", at least it will not appear straight as seen from flat space. Using an exact mathematical description of curved space, the light beam will follow a geodesic. Using a more illustrative idea, because of its mass the light beam will be deflected by a certain angle. The first reliable measurements were performed during a total solar eclipse in 1919 [Sex87]. They showed that the apparent positions of stars whose light was passing the darkened sun were farther away from the sun than the "real" positions measured in the night. It is possible to calculate the deflection angle assuming that light consists of particles and using the Newtonian theory of gravitation, however, this accounts for only half the measured value.
There is another effect involved that can only be explained with general relativity. As it is the case in materials with different refraction indices, light will "avoid" regions in which its apparent speed is reduced. A "detour" may therefore become a "shortcut". This is what happens in the vicinity of a star and what is responsible for the other 50% of the light deflection.
Now we can see the relation of time dilation, length contraction, the geometry of space and the speed of light. A light beam would have a definite speed c=r/t in the "flat" space in some distance from the center of mass. Closer to the center, space itself is "curved", and this again is equivalent to the effect that everything coming from outside would apparently "shrink". A ruler with a length r would appear shortened to r*. Since the time t* is shortened with respect to t by the same factor, c=r/t=r*/t* remains constant. This is what an observer inside the gravity well would measure, and what the external observer would confirm. On the other hand, the external observer would see that the light inside the gravity well takes a detour (judging from his geometry of flat space) *or* would pass a smaller effective distance in the same time (regarding the shortened ruler) *and* the light beam would be additionally slowed down because of the time dilation. Thus, he would measure that the light beam actually needs a longer time to pass by the gravity well than t=r/c. If he is sure about the distance r, then the effective c* inside the gravity well must be smaller:
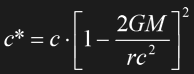
Eq. 1.19
It was confirmed experimentally that a radar signal between Earth and Venus takes a longer time than the distance between the planets indicates if it passes by close to the sun.
Black holes
Let us have a look at Eq. 1.16 and Eq. 1.18 again. Obviously something strange happens at r=2GM/c2. The time t* becomes zero (and the time dilation infinite), and the length x* is contracted to zero. This is the Schwarzschild radius or event horizon, a quantity that turns up in several other equations of GR. A collapsing star whose radius shrinks below this event horizon will become a black hole. Specifically, the space-time inside the event horizon is curved in a way that every particle will inevitably fall into its center. It is unknown how dense the matter in the center of a black hole is actually compressed. The mere equations indicate that the laws of physics as we know them wouldn't be valid any more (singularity). On the other hand, it doesn't matter to the outside world what is going on inside the black hole, since it will never be possible to observe it.

Fig. 1.17 Sequence of events as a person enters a black hole
The sequence of events as a starship passenger approaches the event horizon is illustrated in Fig. 1.17. The lower left corner depicts what an external observer would see, the upper right corner shows the perception of the person who falls into the black hole. Entering the event horizon, he would get a distorted view of the outside world at first. However, while falling towards the center, the starship and its passenger would be virtually stretched and finally torn apart because of the strong gravitational force gradient. An external observer outside the event horizon would perceive the starship and its passenger move slower the closer they get to the event horizon, corresponding to a time dilatation. Eventually, they would virtually seem to stand still exactly on the edge of the event horizon. He would never see them actually enter the black hole. By the way, this is also a reason why a black hole can never appear completely "black". Depending on its age, the black hole will still emit a certain amount of (red-shifted) radiation, aside from the Hawking radiation generated because of quantum fluctuations at its edge.
1.7 Examples of Relativistic Travel
A trip to Proxima Centauri
As already mentioned in the introduction, it is essential to overcome the limitations of special relativity to allow sci-fi stories to take place in interstellar space. Otherwise the required travel times would exceed a person's lifespan by far.
Side note Several of the equations and examples in this sub-chapter are taken from [Ger89].
Let us assume a starship with a very advanced, yet slower-than-light (STL) drive, were to reach Proxima Centauri, about 4ly away from Earth. This would impose an absolute lower limit of 4 years on the one-way travel. However, considering the drastic increase of mass as the ship approaches c, an enormous amount of energy would be necessary. Moreover, we have to take into account a limited engine power and the limited ability of humans to cope with excessive accelerations. A realistic STL travel to a nearby star system could work with a turn-around starship as shown in Fig. 1.13 which will be assumed in the following.
To describe the acceleration phase as observed from Earth's frame of reference, the simple relation v=gt for non-relativistic movements has to be modified as follows:
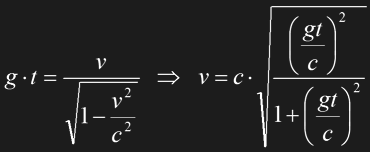
Eq. 1.20
Side note It's not surprising that the above formula for the effective acceleration is also determined by the factor gamma, yet, it requires a separate derivation that I don't further explain to keep this chapter brief.
The relativistic and (hypothetical) non-relativistic speeds at a constant acceleration of g=9.81ms-2 are plotted over time in Fig. 1.18. It would take 409 days to achieve 0.5c and 2509 days to achieve 0.99c at a constant acceleration of g. It is obviously not worth while extending the acceleration phase far beyond 0.5c where the curves begin to considerably diverge. It would consume six times the fuel to achieve 0.99c instead of 0.5c, considering that the engines would have to work at a constant power output all the time, while the benefit of covering a greater distance wouldn't be that significant.
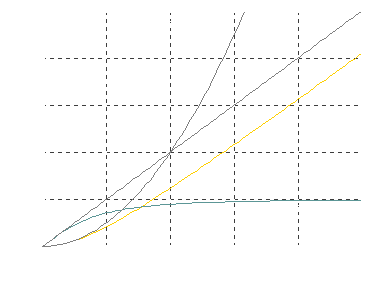
Fig. 1.18 Comparison of Newtonian and relativistic movement
To obtain the covered distance x after a certain time t, the speed v as given in Eq. 1.20 has to be integrated over time:
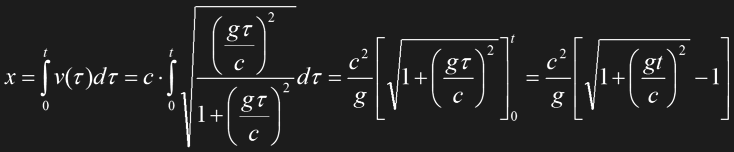
Eq. 1.21
Side note Note that the variable tau instead of t is only used to keep the integration consistent and satisfy mathematicians ;-), since t couldn't denote both the variable and the constant.
There are two special cases which also become obvious in Fig. 1.18: For small speeds gt<<c Eq. 1.21 becomes the Newtonian formula for accelerated movement x=½gt2. Therefore the two curves for non-relativistic and relativistic distances are almost identical during the first few months (and v<0.5c). If the theoretical non-relativistic speed gt exceeds c (which would be the case after several years of acceleration), the formula may be approximated with the simple linear relation x=ct, and the according graph is a straight line. This is evident, since we can assume the ship has actually reached a speed close to c, and the effective acceleration is marginal. A distance of one light-year would then be bridged in slightly more than a year.
If the acceleration is suspended at 0.5c after the aforementioned 409 days, the distance would be 4.84 trillion km which is 0.51ly. With a constant speed of 0.5c for another 2509-409=2100 days the ship would cover another 2.87ly, so the total distance would be 3.38ly. On the other hand, after additional 2100 days of acceleration to 0.99c our ship has bridged 56,5 trillion km, or 5.97ly. As we could expect, the constant acceleration to twice the speed is not as efficient as in the deep-sublight region where it should have doubled the covered distance.
A maximum speed of no more than 0.5c seems useful, at least for "close" destinations such as Proxima Centauri. With an acceleration of g=9.81ms-2 the flight plan could look as follows:
| Flight to Proxima Centauri | Speed | Distance | Earth time | Ship time |
| Acceleration @ g | 0 to 0.5c | 0.51ly | 1.12 years | 0.96 years |
| Constant speed | 0.5c | 2.98ly | 5.96 years | 5.12 years |
| Deceleration @ -g | 0.5c to 0 | 0.51ly | 1.12 years | 0.96 years |
| Total | - | 4ly | 8.20 years | 7.04 years |
Tab. 1.1 Flight plan for an STL trip to Proxima Centauri
The table already includes a correction of an "error" in the above considerations which referred to the time t as it elapses on Earth. The solution of the twin paradox revealed that the space traveler who leaves Earth at a certain speed and stops at the destination changes their frame of reference each time, no matter whether or not we take into account the effects of the acceleration phases. This is why the special relativistic time dilatation will become asymmetric. As the space traveler returns to Earth's frame of reference -either by returning to Earth or by landing on Proxima Centauri which can be supposed to be roughly in the same frame of reference as Earth- he will have aged less than his twin on Earth. During his flight his ship time t* elapses slower than the time t in Earth's frame of reference:

Eq. 1.22
Eq. 1.22 is valid if the speed v is constant. During his constant speed period of 5.96 years in Earth's frame of reference the space traveler's clock would proceed by 5.12 years. In case of an acceleration or deceleration we have to switch to infinitesimal time periods dt and dt* and replace the constant velocity v with v (t) as in Eq. 1.20. This modified equation has to be integrated over the Earth time t to obtain t*:
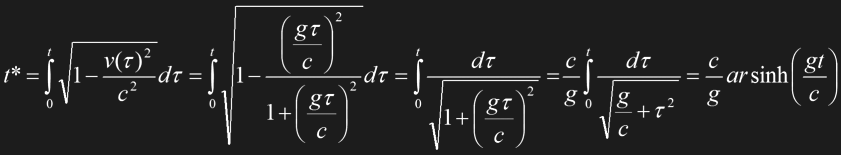
Eq. 1.23
Side note The function arsinh is called "area sinus hyperbolicus".
The space traveler would experience 0.96 years during the acceleration as well as the deceleration. The times are summarized in Tab. 1.1, yielding a total time experienced by the ship passenger of 7.04 years, as opposed to 8.20 years in the "resting" frame of reference on Earth.
Traveling to the edge of the universe
The prospect of slowing down time as the ship approaches c offers fascinating possibilities of space travel even without FTL drive. The question is how far an STL starship could travel within a passenger's lifetime, assuming a constant acceleration of g=9.81ms-2 all the time. Provided there is a starship with virtually unlimited fuel, the following theory would have to be proven: If the space traveler continued acceleration for many years, his speed would very slowly approach, but never exceed c, if observed from Earth. This wouldn't take him very far in his lifetime. However, according to Eq. 1.23 time slows down more and more, and this is the decisive effect. We might want to correct the above equations with the slower ship time t* instead of the Earth time t. We obtain the ship speed v* and distance x* if we apply Eq. 1.23 to Eq. 1.20 and Eq. 1.21, respectively.
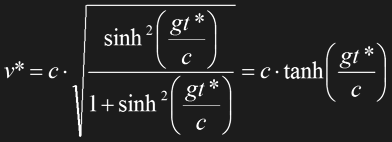
Eq. 1.24
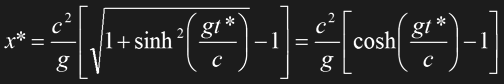
Eq. 1.25
Note that the term tanh (gt*/c) is always smaller than 1, so that the measured speed always remains slower than c. On the other hand, x* may rise to literally astronomical values. Fig. 1.19 depicts the conjectural travel to the edge of the universe, roughly 10 billion light-years away, which could be accomplished in only 25 ship years! The traveler could even return to Earth which would require another 25 years; but there wouldn't probably be much left of Earth since the time elapsed in Earth's frame of reference would sum up to 10 billion years, obviously the same figure as the bridged distance in light-years.
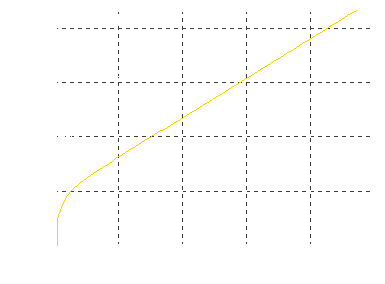
Fig. 1.19 Plan for an STL trip to the edge of the universe
Side note Apart from the objection that there would be hardly unlimited fuel for the travel, the above considerations assume a static universe. The real universe would further expand, and the traveler could never reach its edge which is probably moving at light speed.
Fuel problems
The non-relativistic relation of thrust and speed was discussed in Section 1.5. If we take into account relativistic effects, we see that at a constant thrust the effective acceleration will continually decrease to zero as the speed approaches c. The simple relation v=gt is not valid anymore and has to be replaced with Eq. 1.20. Thus, we have to rewrite the fuel equation as follows:
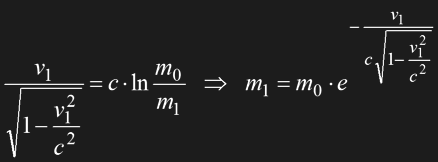
Eq. 1.26
The two masses m0 and m1 still denote non-relativistic rest masses of the ship before and after the acceleration, respectively. Achieving v1=0.5c would require not much more fuel than in the non-relativistic case, the payload could still be 56% of the total mass compared to 60%. This would be possible, provided that a matter/antimatter power source is available and the power conversion efficiency is 100%. If the aspired speed were 0.99c, the ship would have an unrealistic fuel share of 97%. The flight to the edge of the universe (24 ship years at a constant apparent acceleration of g) would require a fuel mass of 56 billion times the payload which is beyond every reasonable limitations, of course.
If we assume that the ship first accelerates to 0.5 and then decelerates to zero on the flight to Proxima Centauri, we will get a still higher fuel share. Considering that Eq. 1.26 only describes the acceleration phase, the deceleration would have to start at a mass of m1, and end at a still smaller mass of m2. Taking into account both phases, we will easily see that the two mass factors have to be multiplied:
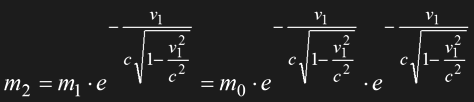
Eq. 1.27
This would mean that the payload without refueling could be only 31% for v1=0.5c. For v1=0.99c the ship would consist of virtually nothing but fuel. Just for fun, flying to the edge of the universe and landing somewhere out there would need a fuel of 3*1021 tons, if the payload is one ton (Earth's mass: 6*1021t).















